PolyPose

Overview

Deformable 2D/3D registration is a long-standing challenge. The central obstacle is that soft tissues have very poor contrast on X-ray. As such, it’s nearly impossible to estimate their intricate deformations from a handful of (i.e., less than 10) 2D X-rays.

PolyPose overcomes this limitation by parameterizing complex 3D deformation fields as a composition of rigid transforms, exploiting the biologic constraint that bones do not bend in typical motion. For example, in the scene below, combining the optimized transforms of a few rigid bodies yields a detailed, smooth (it’s actually diffeomorphic by construction!), and accurate deformation field.

Contributions

The key advantages of PolyPose are:

• Our low-dimensional model is far easier to optimize than dense displacement fields, while being just as expressive.
• Our method is regularizer- and hyperparameter-free, enabling out-of-the-box generalization to new procedures.
• Our anatomically motivated model is robust in challenging sparse-view and limited-angle settings.

Results

Sparse-view 2D/3D registration in radiotherapy

PolyPose could be very useful in radiotherapy by matching a pre-interventional 3D radiation plan to the patient’s current position in the treatment room. We demonstrate the capability of PolyPose to track sensitive soft tissues in X-ray using the Head&Neck dataset, a collection of longitudinal CTs from patients with head and neck squamous cell carcinoma.

The figure below shows warped CTs produced by different 2D/3D and 3D/3D registration algorithms from 3 input X-ray images. PolyPose estimates the most accurate deformation fields the highest 3D Dice on both rigid structures and important soft tissue organs, even though the pose of these organs was not directly estimated during optimization!

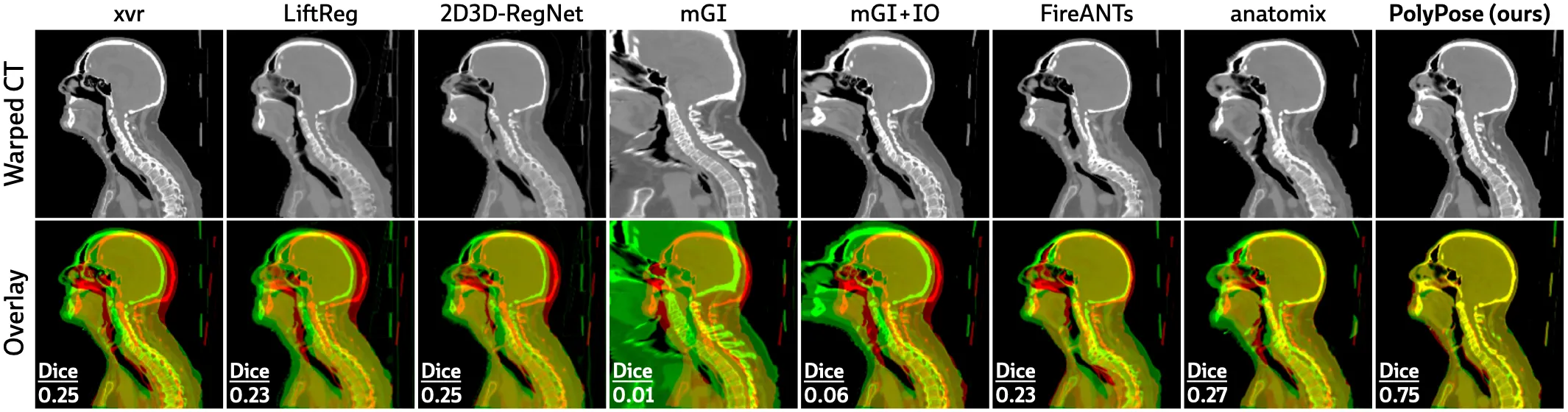
The deformation fields estimated by PolyPose also have minimal topological defects. Because our warps are constructed from a small number of rigid components, their deformation fields are more interpretable and anatomically plausible than the baselines.

Limited-angle 2D/3D registration in orthopedic surgery

PolyPose is also amenable to many applications in orthopedic surgery, where tracking the soft tissue deformations induced by multiple articulated structures is a central challenge. Using the DeepFluoro dataset, we show that PolyPose can successfully register a CT to a pair of X-ray images spaced only ~30° apart.

Below, we compare PolyPose to two other parameterizations of a dense deformation field: per-voxel $\mathbf{SE}(3)$ transformations and translations, also optimized via differentiable rendering. These dense deformation parameterizations estimate warps that reproduce the appearance of the training X-rays, achieving much higher image similarity metrics than PolyPose.

However, if you compare the estimated warps below (these are 3D models, click and drag them!), you can see that only PolyPose successfully recovers the true anatomical motion in this scene (i.e., external rotation of the femurs).

This is because PolyPose has only $\mathcal O(K)$ optimizable parameters and is thus well suited for ill-posed settings, whereas the under-constrained dense representations have $\mathcal O(M)$ parameters with $K \ll M$. Here, $K=3$ and $M = 398 \times 197 \times 390 \approx 10^7$.

Methods

The inputs to our method are a preoperative 3D CT volume $\mathbf{V}$ and a series of intraoperative 2D X-ray images $\mathbf{I}_1, \dots, \mathbf{I}_N$. These data are related by the following image formation model:

This equation can be understood as first warping the volume with a deformation field $\mathbf\Phi: \mathbb R^3 \to \mathbb R^3$, then rendering a 2D X-ray image with a projector $\mathcal P$ oriented via the camera matrix $\mathbf \Pi_n$.

Given $\mathbf{V}$ and $\mathbf{I}$ , our goal is to solve for the camera matrices $\mathbf \Pi_1, \dots, \mathbf \Pi_N$ and the deformation field $\mathbf \Phi$.

Estimating the camera matrices $\mathbf\Pi_1, \dots, \mathbf\Pi_N$

Accurately estimating the pose of each 2D X-ray image relative to the 3D volume is of vital important for downstream estimation of the non-rigid deformation field. If these camera matrices are miscalibrated, we cannot hope to recover the deformation field $\mathbf \Phi$.

For this critical task, we use xvr, the current state-of-the-art method for rigid 2D/3D registration, which enables fully automatic submillimeter-accurate C-arm pose estimation. Specifically, we estimate camera matrices by rigidly aligning an anchor structure that is reliably visible in the preoperative 3D volume and all intraoperative 2D views (e.g., the pelvis in the figure below).

Optimizing the polyrigid deformation field $\mathbf\Phi$

Armed with accurate camera matrices, we can now fit a polyrigid deformation model!

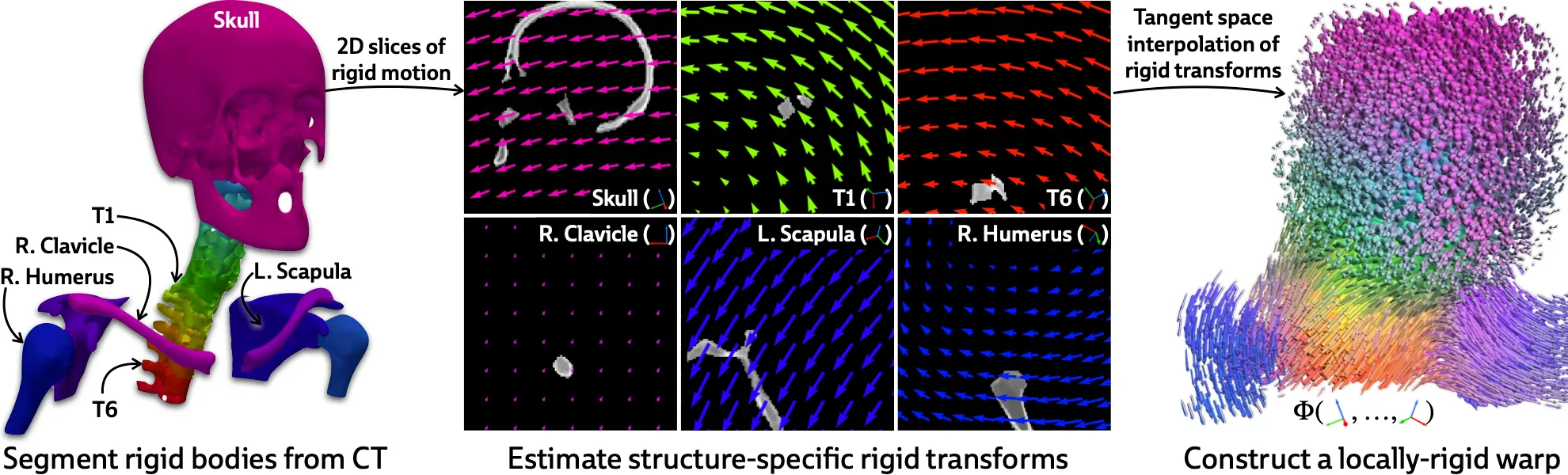
The first step is to get a rough segmentation of the rigid bodies in the 3D CT volume (I say “rough” because our ablations show that PolyPose is robust to massive segmentation errors). For most structures, this can be done with automated tools like TotalSegmentator; applications to more unusual structures may wish to leverage semi-automated segmentation tools like nnInteractive. Regardless, with a 3D segmentation of $\mathbf V$, we can compute a 3D weight field, which models how much every voxel is influenced the different rigid bodies as a function of distance.

With this weight field, we can finally define the polyrigid transform that we wish to optimize:

That is, polyrigid deformations are locally linear transforms, where the displacement at each voxel is given by a weighted average (hence the weight field) of the rigid transforms of all rigid bodies in the volume! Therefore, the only thing we need to optimize are the structure-specific rigid transforms. The optimization process if visualized below:

A neat implementation trick…

If you inspect the formula for a polyrigid deformation, you’ll notice that we don’t operate directly on rigid transformations, but rather on their log-transformed counterparts living in the tangent space $\mathfrak{se}(3)$. This yields a very simple implementation, which is demonstrated in pseudocode below (you can find the full implementation here):

    
    def polyrigid_deformation_field(
    volume: Float[torch.Tensor, "D H W"],  # A volume with C rigid bodies
    weights: Float[torch.Tensor, "C D H W"],  # Weight field for the volume
    log_poses: Float[torch.Tensor, "C N"],  # Log-transformed poses for the rigid bodies
    pts: Float[torch.Tensor, "D H W 3"],  # Coordinates of the volume's voxels
) -> Float[torch.Tensor, "D H W"]:
    weighted_log_poses = einsum("cdhw, cn -> dhwn", weights, log_poses)
    polyrigid_poses = exp(weighted_log_poses)
    deformation_field = polyrigid_poses(pts)
    warped_volume = grid_sample(volume, deformation_field)
    return warped_volume
  

…and a final fun GIF ☠️

Shows the evolution of a polyrigid deformation field over the first few iterations of optimization.

Future Work

There are many interesting extensions that could be made to PolyPose! For example, one could enforce skeleton constraints, requiring that all rigid bodies connected at joints influence each other via a kinematic chain. As demonstrated by the initial implementation in PolyPose, enforcing physics-based priors makes models more robust in sparse-data settings.

Additionally, the warped CTs produced by the estimated deformation fields could be used to initialize post-hoc 3D image reconstruction techniques (e.g., using differentiable rendering techniques such as DiffVox). This approach could be used to reconstruct changes from the preoperative to the intraoperative state in 3D (e.g., implanted devices, altered morphology, etc.).

BibTeX citation

    
    @misc{gopalakrishnan2025polypose,
  title={PolyPose: Deformable 2D/3D Registration via Polyrigid Transforms},
  author={Gopalakrishnan, Vivek and Dey, Neel and Golland, Polina},
  journal={Advances in Neural Information Processing Systems},
  year={2025}
}